Statistiek
We gebruiken statistiek om gegevens beter te kunnen begrijpen. Dit kunnen we doen door het op een begrijpelijke manier weer te geven. Bijvoorbeeld in een staafdiagram, histogram of een cirkeldiagram. Maar we kunnen ook bepaalde gegevens berekenen die ons helpen de data beter te begrijpen. Bijvoorbeeld het gemiddelde, de mediaan of de modus geeft ons een beeld van hoe de data eruit ziet. Dit is handig, want dan hoeven we niet alles te zien, maar we kunnen toch iets over deze data zeggen. Ook is dit handig als we data willen vergelijken.
Data weergeven
We kunnen informatie handig weergeven in grafieken en in diagrammen. We kijken naar een paar verschillende type diagrammen en bekijken hoe je ze af moet lezen en zelf maken.
Staafdiagrammen
We beginnen met staafdiagrammen. Laten we naar een voorbeeld kijken om te zien hoe het werkt. Dus stel we willen kijken naar het aantal fietsen dat een fietsenwinkel verkoopt in 1 week. We krijgen de volgende data:
| Dag | Aantal fietsen |
|---|---|
| Maandag | 8 |
| Dinsdag | 5 |
| Woensdag | 9 |
| Donderdag | 4 |
| Vrijdag | 15 |
| Zaterdag | 24 |
| Zondag | 11 |
Hoe kunnen we dit nu op een handige en duidelijke manier weergeven? We kunnen dit doen met een staafdiagram. In Figuur 1 is er een staafdiagram weergegeven van deze data.

Hiermee kunnen we precies zien hoeveel fietsen er op elke dag zijn verkocht. Ook zien we meteen op welke dag de meeste fietsen zijn verkocht en op welke dag de minste fietsen.
We zien dat er op zaterdag de meeste fietsen zijn verkocht, want die staaf is het hoogst. We kunnen ook zien dat er toen 24 fietsen verkocht waren. Verder kunnen we ook zien dat op donderdag de minste fietsen zijn verkocht, want die staaf is het kleinst. Er waren namelijk toen maar 4 fietsen verkocht.
Belangrijk
Wanneer gebruiken we een Staafdiagram?
- Frequentie van verschillende groepen of categorieën willen weergeven en vergelijken.
- Frequenties willen vergelijken van dezelfde groep met meerdere datasets.
In ons voorbeeld is elke dag een andere groep en is de frequentie het aantal fietsen. We zien dus hoeveel fietsen (frequentie) er verkocht zijn per dag (groep).
Histogrammen
Laten we nu kijken naar een klas die een wiskunde toets heeft gemaakt. De leerlingen hebben dus allemaal verschillende cijfers gehaald. We kunnen die data weergeven met een zogenaamde histogram. In Figuur 2 zien we hoe dit eruit ziet.

Dus \(4\) leerlingen hebben een \(4\) gehaald, \(8\) leerlingen hebben een \(7\) gehaald en \(3\) leerlingen hebben een \(9\) gehaald.
Belangrijk
Wanneer gebruiken we een Histogram?
- Continue dataverdeling willen weergeven.
- Meerdere datasets tegelijk willen weergeven.
- Verdelingen van verschillende datasets willen vergelijken.
In ons voorbeeld gaat de cijferverdeling van een 4 naar een 9. Dus de leerlingen hebben allemaal tussen een 4 en een 9 gehaald voor de wiskunde toets. En we kunnen dan precies zien hoeveel leerlingen een bepaald cijfer hebben gehaald.
Cirkeldiagrammen
We kunnen het voorbeeld van net ook weergeven in een zogenaamde cirkeldiagram.

In Figuur 3 kunnen we zien welk deel van de leerlingen een bepaald cijfer heeft gehaald. Dus \(26.7\%\) heeft een \(7\) gehaald, \(20\%\) een heeft een \(8\) gehaald, \(10\%\) heeft een \(9\) gehaald, etc.
Belangrijk
Wanneer gebruiken we een Cirkeldiagram?
- (Een klein aantal) verschillende groepen willen vergelijken.
- Vooral de relatieve/procentuele verschillen willen weergeven.
We kunnen nu dus goed zien welk deel van de leerlingen een bepaald cijfer heeft gehaald. Maar we kunnen niet meer meteen zien hoeveel dat er waren. We kunnen dus niet meer meteen zien dat het 8 leerlingen waren die een 7 hebben gehaald. We kunnen alleen maar zien dat het \(26.7\%\) is van alle leerlingen.
Lijndiagrammen
De laatste manier om data weer te geven is met een lijndiagram. We kijken nu naar de temperatuur in de maand Juli.

We kunnen in Figuur 4 precies aflezen wat de minimum temperatuur en wat de maximum temperatuur is op elke dag in Juli. Dus op \(10\) Juli was de minimum temperatuur ongeveer \(23 \ ^{\circ} \textrm C\) en de maximum temperatuur ongeveer \(29 \ ^{\circ} \textrm C\).
Belangrijk
Wanneer gebruiken we een Lijndiagram?
- Een verband tussen twee waardes willen weergeven.
- Meerdere datasets met dezelfde grootheden tegelijk willen weergeven.
In dit geval kijken we naar het verband tussen de grootheden temperatuur en tijd. We kunnen dan precies zijn hoe de temperatuur verandert in de tijd. We vergelijken ook meerdere datasets met dezelfde grootheden. We kijken namelijk naar de maximum temperatuur en de minimum temperatuur per dag. Dus beide datasets hebben de grootheden temperatuur en tijd, maar met verschillende waardes.
Gemiddelde
Het gemiddelde is handig om iets te kunnen zeggen over de hele dataset. Over het algemeen kun je dan kijken waar de meeste data zich bevindt. Dit maakt het vergelijken van verschillende datasets makkelijker.
Laten we bijvoorbeeld naar twee verschillende klassen kijken: klas A en klas B. De twee klassen hebben net een toets gemaakt en alle leerlingen hebben hun cijfer terug. De cijfers van beide klassen is weergegeven in een histogram in Figuur 5.

We zien hier dat de cijfers van klas A over het algemeen hoger zijn dan die van klas B. Maar hoeveel beter heeft klas A het over het algemeen gedaan? Om dit te bekijken, is het handig om de gemiddeldes te berekenen en die te vergelijken.
We berekenen een gemiddelde op de volgende manier:
Belangrijk
Gemiddelde berekenen
1. Tel alle getallen bij elkaar op.
2. Deel het door het aantal getallen.
Simpel Voorbeeld
Voor de getallen \(2, 4, 6, 8\) kunnen we het gemiddelde als volgt berekenen:
1. We tellen alle getallen bij elkaar op:
2. Dan delen we het door het aantal getallen:
Het gemiddelde van deze reeks getallen is dus \(5\).
Om het gemiddelde van de twee klassen te bepalen moeten we dus eerst alle cijfers van alle leerlingen bij elkaar op tellen. Hiervoor moeten we voor elk cijfer weten hoeveel leerlingen dat cijfer hebben gehaald. Uit Figuur 5 kunnen we de volgende tabel maken:
Klas A
| Cijfers | Frequentie |
|---|---|
| 4.5 | 5 |
| 5.0 | 4 |
| 5.5 | 5 |
| 6.0 | 6 |
| 6.5 | 7 |
| 7.0 | 7 |
| 7.5 | 9 |
| 8.0 | 8 |
| 8.5 | 6 |
| 9.0 | 4 |
| 9.5 | 1 |
Klas B
| Cijfers | Frequentie |
|---|---|
| 3.0 | 5 |
| 3.5 | 6 |
| 4.0 | 9 |
| 4.5 | 10 |
| 5.0 | 11 |
| 5.5 | 9 |
| 6.0 | 8 |
| 6.5 | 7 |
| 7.0 | 3 |
Om nu het gemiddelde te berekenen, berekenen we eerst de som van alle cijfers. We beginnen met klas A. Om dit te doen moeten we dus alle cijfers van alle leerlingen bij elkaar op tellen. We kunnen dit doen door steeds het cijfer keer het aantal mensen met dat cijfer te doen. En dit kunnen we dan allemaal bij elkaar optellen:
\(\textrm{Som cijfers klas A} = 5 \times 4.5 + 4 \times 5.0 + 5 \times 5.5 + 6 \times 6.0 + 7 \times 6.5 + 7 \times 7.0\)
\(\phantom{\textrm{Som cijfers klas A ...}} + 9 \times 7.5 + 8 \times 8.0 + 6 \times 8.5 + 4 \times 9.0 + 1 \times 9.5\)
Nu berekenen we het totaal aantal leerlingen. Dit doen we door alle frequenties bij elkaar op te tellen. Elke leerling heeft namelijk maar 1 cijfer gehaald. Dus het aantal behaalde cijfers is dan ook meteen het aantal leerlingen.
We kunnen nu het gemiddelde berekenen door deze twee waardes door elkaar te delen:
Het gemiddelde van klas A is dus een \(6.9\).
Om het gemiddelde van klas B te bepalen doen we precies dezelfde stappen:
We tellen eerst weer alle cijfers keer hun frequentie bij elkaar op:
\(\textrm{Som cijfers klas B} = 5 \times 3.0 + 6 \times 3.5 + 9 \times 4.0 + 10 \times 4.5 + 11 \times 5.0 + 9 \times 5.5\)
\(\phantom{\textrm{Som cijfers klas B ...}} + 8 \times 6.0 + 7 \times 6.5 + 3 \times 7.0\)
Het totaal aantal leerlingen is alle frequenties bij elkaar opgeteld:
En het gemiddelde wordt dan:
Het gemiddelde van klas B is dus een \(4.9\).
Het gemiddelde van klas A is dus \(2\) cijferpunten hoger dan die van klas B. Dus over het algemeen heeft een leerling uit klas A \(2\) cijferpunten hoger gehaald dan een leerling uit klas B.

Voorbeelden
Voorbeeld 1: Gemiddelde temperatuur eerste week December
Bereken de gemiddelde temperatuur in de eerste week van December.
De temperaturen van de eerste week van December zijn weergegeven in Figuur 1. Wat is de gemiddelde temperatuur van deze week?

Uitwerking
We maken eerst een tabel van de temperatuur op elke dag. Hiermee kunnen we namelijk de gemiddelde temperatuur makkelijker berekenen.
| Dag | Temperatuur (°C) |
|---|---|
| 1 | -3.7 |
| 2 | 3.5 |
| 3 | 2.6 |
| 4 | -2.4 |
| 5 | 0.0 |
| 6 | -0.5 |
| 7 | 1.5 |
Nu kunnen we het gemiddelde berekenen. We bepalen eerst de som van alle temperaturen:
Nu moeten we dit delen door het aantal dagen, dus door \(7\). We vinden dan als gemiddelde:
Als we dit tekenen in Figuur 1, dan kunnen we controleren of ons antwoord een beetje logisch is. En inderdaad, dit antwoord zou best wel eens kunnen kloppen.

Voorbeeld 2: Gemiddelde lengte van groep jongens en meisjes
Bereken de gemiddelde lengte van een groep met 5 jongens en 5 meisjes.
Een groep van 5 jongens en 5 meisjes meten allemaal hun lengte. De metingen zijn weergegeven in de onderstaande tabel.
Bereken de gemiddelde lengte van de jongens en de gemiddelde lengte van de meisjes. Hoeveel zijn de jongens gemiddeld langer dan de meisjes?
| Lengte Meisje (cm) | Lengte Jongen (cm) | ||||
|---|---|---|---|---|---|
| 1 | 161 | 1 | 176 | ||
| 2 | 167 | 2 | 182 | ||
| 3 | 172 | 3 | 187 | ||
| 4 | 154 | 4 | 171 | ||
| 5 | 176 | 5 | 191 |
Uitwerking
We beginnen met de gemiddelde lengte te berekenen van de meisjes. We beginnen met alle lengtes bij elkaar op te tellen:
Om het gemiddelde te berekenen delen we de som door het totaal aantal meisjes, dus door \(5\):
We herhalen deze stappen ook voor de jongens:
Nu delen we de som weer door het totaal aantal jongens, dus ook door \(5\):
We kunnen nu bepalen hoeveel de jongens gemiddeld langer zijn dan de meisjes. We doen de gemiddelde lengte van de jongens min de gemiddelde lengte van de meisjes:
Dus de jongens zijn gemiddeld \(15.4\) cm langer dan de meisjes.
Voorbeeld 3: Gemiddelde leeftijd
Bereken de gemiddelde leeftijd van kleinkinderen met én zonder hun grootouders.
Er zijn wat kleinkinderen op bezoek bij hun opa en oma. De kleinkinderen en hun grootouders verschillen best veel van leeftijd.
Bereken de gemiddelde leeftijd van de kleinkinderen met hun grootouders. Bereken ook de gemiddelde leeftijd van de kleinkinderen zonder hun grootouders.
Hoeveel neemt het gemiddelde af als we de grootouders weglaten?
| Persoon | Leeftijd |
|---|---|
| 1 | 78 |
| 2 | 74 |
| 3 | 17 |
| 4 | 15 |
| 5 | 19 |
| 6 | 24 |
| 7 | 11 |
| 8 | 21 |
Uitwerking
Om het gemiddelde te berekenen, tellen we eerst alle leeftijden bij elkaar op en dan delen we door het aantal mensen. We beginnen met het gemiddelde berekenen met de grootouders erbij.
Het totaal aantal mensen met grootouders erbij is \(8\), en dus moeten we door \(8\) delen. Het gemiddelde wordt dus:
Nu bereken we het gemiddelde zonder de grootouders. We berekenen eerst de som:
Er zijn \(6\) kleinkinderen en dus delen we door \(6\).
Als we de grootouders weglaten, neemt het gemiddelde dus af met ongeveer:
Voorbeeld 4: Gemiddelde van cijfers met weging
Bereken het gewogen gemiddelde van alle cijfers.
Een leerling heeft de volgende cijfers gehaald (zie Figuur 2). Wat staat de leerling gemiddeld voor alle vakken samen als we de weging van de cijfers meenemen?
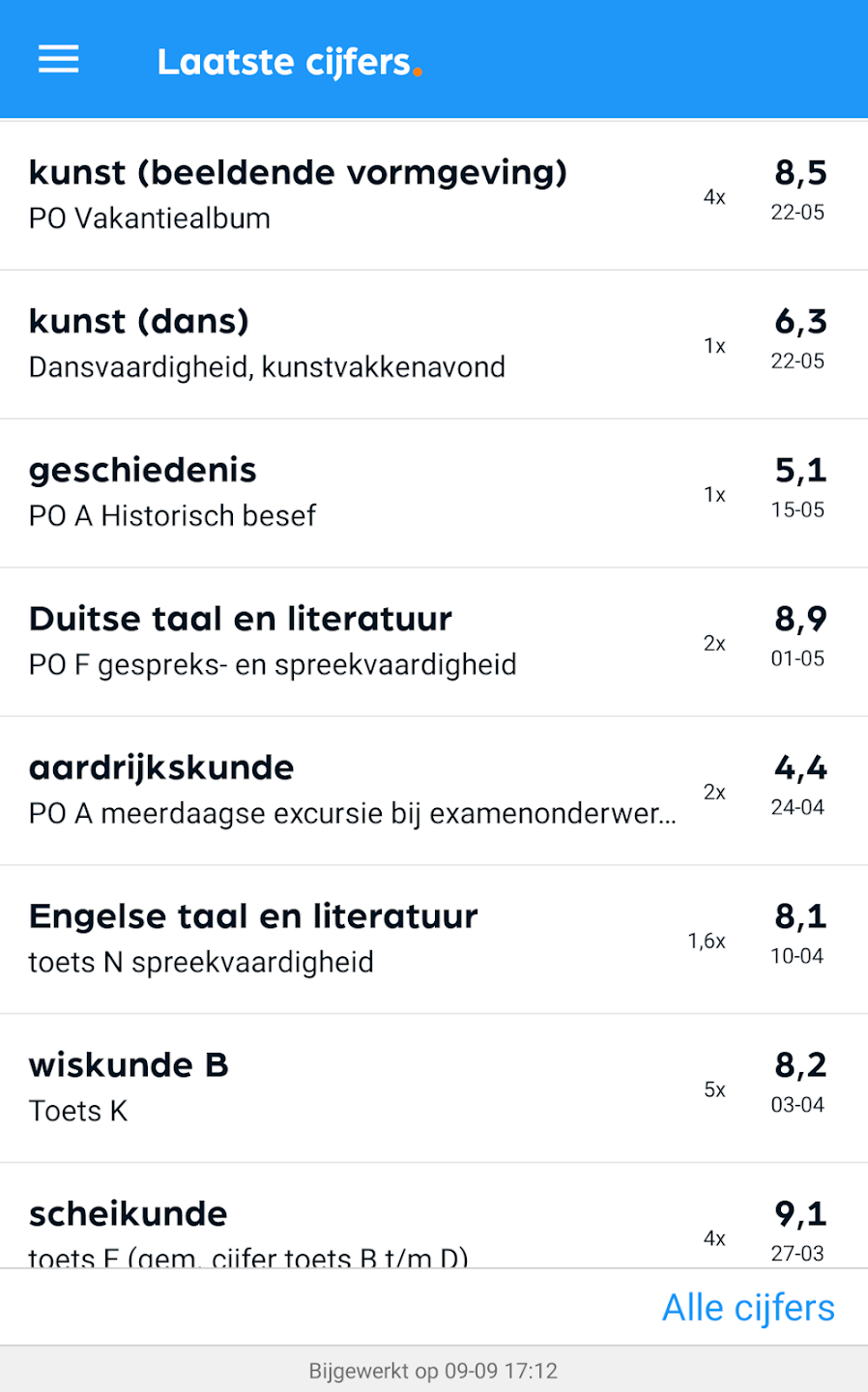
Om het gemiddelde te berekenen, berekenen we eerst de som van alle cijfers. We willen het gewogen gemiddelde, dus moeten we de cijfers een weging meegeven.
Dit doen we door alle individuele cijfers te vermenigvuldigen met hun weging. Hoe zwaarder de weging, hoe meer het gemiddelde erdoor wordt beïnvloed:
\(\large{\textrm{Som} = 4 \times 8.5 + 1 \times 6.3 + 1 \times 5.1 + 2 \times 8.9 + \phantom{.}}\)
\(\large{\phantom{\textrm{Som ....}} 2 \times 4.4 + 1.6 \times 8.1 + 5 \times 8.2 + 4 \times 9.1}\)
Als we het aantal cijfers willen bepalen, dan moeten we de wegingen bij elkaar op tellen. Dit doen we zodat we niet opeens een cijfer krijgen dat hoger is dan een \(10\).
\(\large{\textrm{Aantal cijfers} = 4 + 1 + 1 + 2 + 2 + 1.6 + 5 + 4}\)
Nu delen we de som door het aantal cijfers om het gemiddelde te berekenen:
Het gewogen gemiddelde van de cijfers is dus een \(7.9\).
Mediaan en Modus
We hebben net gezien dat een gemiddelde heel erg handig kan zijn om data te vergelijken. Maar soms kan het gemiddelde juist een verkeerd beeld geven. Laten we kijken naar inkomens van \(100\) mensen waar er \(1\) biljonair bij zit. In Figuur 6 is het inkomen weergegeven van de andere \(99\) mensen.

Nu voegen we aan deze groep mensen de biljonair toe die een inkomen heeft van \(1\) miljard euro. Nu berekenen we het gemiddelde. Als we dit doen, dan vinden we het volgende:
Het gemiddelde is dus ongeveer 10 miljoen euro! Maar dit is een vertekend beeld, want bijna niemand uit deze groep komt in de buurt van dit gemiddelde. De biljonair zorgt er dus voor dat het gemiddelde heel erg hoog wordt. Het gemiddelde is dus erg gevoelig voor extreem hoge of extreem lage waardes. Daarom is het in dit geval handiger om de mediaan te gebruiken.
Belangrijk
Mediaan bepalen
De mediaan is de middelste waarde uit een dataset wanneer de data gesorteerd is van laag naar hoog. Dus om de mediaan te bepalen moeten we het volgende doen:
1. Sorteer de data van laag naar hoog.
2. Is de data oneven? \(\Longrightarrow\) Kies het middelste getal.
\(\phantom{..}\) Is de data even? \(\Longrightarrow\) Bereken het gemiddelde van de middelste twee getallen.
Simpel Voorbeeld: Mediaan
Oneven dataset
We willen van deze dataset de mediaan bepalen. Hoe doen we dat?
We beginnen met het sorteren van laag naar hoog:
Deze data set is oneven en dus kunnen we gelijk het middelste getal kiezen. In dit geval is dit \(4\) en dus is onze mediaan \(4\).
Even dataset
Stel we hebben nu de volgende dataset:
Nu willen we weer de mediaan bepalen. Dus we sorteren eerst dit weer van laag naar hoog:
Deze dataset is even en dus moeten we het gemiddelde nemen van de middelste twee getallen. De middelste twee getallen zijn \(5\) en \(8\), dus onze mediaan wordt:
Laten we weer terug gaan naar de inkomens van de groep van 100 mensen. Als we de mediaan willen bepalen, dan moeten we dus alle \(100\) inkomens op volgorde van laag naar hoog zetten. \(100\) is een even getal en dus berekenen we het gemiddelde van de middelste twee waardes. Als we dit doen, dan vinden we als mediaan:
En we zien dat dit meer lijkt op het inkomen van de meeste mensen, in tegenstelling tot het gemiddelde.
Apart van de mediaan, kunnen we ook de modus bepalen om de data beter te begrijpen. De modus vertelt ons welk getal het vaakst voorkomt.
Belangrijk
Modus bepalen
Over de modus:
- De modus is het getal dat het vaakst voorkomt.
- Het is handig om de data te sorteren van laag naar hoog om dit makkelijk te zien.
- Als er twee getallen zijn die allebei het meest voorkomen, dan is er geen modus.
Simpel Voorbeeld: Modus
Modus bepalen
Stel we willen weten wat de modus is van deze getallen, dus welk getal het vaakst voorkomt. Om dat te doen, is het handig om de data te sorteren van laag naar hoog. We vinden dan:
We zien dat het getal \(2\) het vaakst voorkomt en dus is onze modus \(2\).
Geen Modus
Stel we willen weer de modus bepalen van deze dataset:
We sorteren het dan eerst weer van laag naar hoog:
We zien nu dat \(3\) en \(4\) allebei het meest voorkomen en omdat dit meer dan 1 getal is, hebben we geen modus.
Voorbeelden
Voorbeeld 1: Mediaan en Modus van het aantal dobbelsteen ogen
Bepaal de Mediaan en de Modus van het aantal dobbelsteen ogen
Er is meerdere keren met een dobbelsteen gegooid. De uitslagen van het aantal ogen is hier rechts weergegeven in Figuur 1. Wat is de mediaan en wat is de modus van deze worpen?
Uitwerking
Om te bepalen wat de mediaan is, is het handig om het aantal ogen per worp te sorteren van laag naar hoog. Als we dit doen, dan vinden we:
Nu berekenen we de mediaan. Er waren \(12\) worpen en dit is een even getal. We moeten dus de middelste twee getallen nemen en daar het gemiddelde van nemen. De middelste twee getallen zijn:
Het gemiddelde van \(2\) met zichzelf is gewoon \(2\) en dus krijgen we:
Om de modus te bepalen moeten we kijken welk getal het vaakst voorkomt. Met het gesorteerd aantal ogen kunnen we zien dat \(2\) ogen het vaakst is gegooid. De modus is dus \(2\).
Voorbeeld 2: Mediaan en Modus van verschillende schoenmaten
Bepaal de Mediaan en de Modus van de verschillende schoenmaten
Een groep leerlingen heeft allemaal gemeten wat hun schoenmaat is. Dit is weergegeven in Figuur 2. Bepaal van deze data de mediaan en de modus.
Uitwerking
Dit is een even dataset, dus moeten we het gemiddelde nemen van de middelste twee getallen. De middelste twee getallen zijn:
De mediaan is dus het gemiddelde van \(39\) en \(40\):
De modus is het getal dat het vaakst voorkomt. In dit geval komen alle getallen even vaak voor, en is er dus geen modus
Voorbeeld 3: Mediaan en Modus van het aantal huisdieren
Bepaal de Mediaan en de Modus van het aantal huisdieren
Leerlingen uit een klas hebben allemaal doorgegeven hoeveel huisdieren ze hebben. Dit is weergegeven in een histogram in Figuur 3. Bepaal van deze data de mediaan en de modus.

Uitwerking
We kunnen uit Figuur 3 meteen aflezen dat \(1\) huisdier per leerling het vaakst voorkomt en dus is de modus \(1\).
Om de mediaan te bepalen zouden we de data uitkunnen schrijven, maar we kunnen het ook doen met de grafiek. De totaal aantal leerlingen is:
Dit is een even aantal en dus moeten we het gemiddelde nemen van de middelste twee getallen. De middelste twee getallen zijn het \(15^{\textrm{e}}\) en het \(16^{\textrm{e}}\) getal uit de gesorteerde dataset.
In Figuur 3 is de data al gesorteerd. We kunnen daar zien dat we eerst 8 keer 0 huisdieren hebben en daarna 9 keer 1 huisdier. Samen zijn dit de eerste \(17\) getallen van de dataset en dus weten we dat zowel het \(15^{\textrm{e}}\) als het \(16^{\textrm{e}}\) getal \(1\) moet zijn. Het gemiddelde van twee keer hetzelfde getal is het getal zelf, en dus vinden we dat de mediaan \(1\) is.

